[Clustering] RFM지표를 이용한 K-Means Clustering
마케팅 타겟을 분류하는 프로젝트 진행해보려 한다. K-Means Clustering 알고리즘을 활용해, 각 소비자 그룹별 RFM 지표의 특징을 파악해 효율적인 마케팅 전략을 수립해보자!
RFM
- Recency, Frequency, Monetary (거래의 최근성, 빈도, 총액)
- 기존 고객을 분석하고 유지하기 위한 고객 기반 마케팅 분석 지표
- 매출에 있어 거래의 최근성, 빈도, 총액이 가장 중요한 factor라고 가정해 만든 지표
→ 프로젝트를 통해 RFM을 기반으로, 고객의 순위를 지정, 그룹화하여 최고의 고객을 식별하거나 타겟 마케팅 캠페인에 사용하려한다.

Clustering
서로 유사한 데이터들은 같은 그룹으로, 서로 유사하지 않은 데이터는 다른 그룹으로 분리하는 것
K-means Clustering
- centroid based clustering 알고리즘이라고도 불림
- centroid(군집 중심점)라는 특정한 임의의 지점을 선택해 해당 중심점으로부터 거리가 가장 가까운 포인트를 같은 cluster, 즉 비슷한 특성을 가진 데이터들이 모인 집단으로 묶는 방법
- 데이터가 비슷하다 = 데이터 사이들간의 거리가 가깝다
- 데이터들 사이 거리 측정해 그 거리를 기반으로 가까운 데이터들끼리 클러스터로 묶어줌
- 데이터 사이의 거리 계산
- Euclidean distance (일반적으로 가장 많이 쓰임)
- cosine similarity
- jaccard distance
- 방법





Elbow Method
최적의 k, 즉 적절한 cluster의 개수를 찾는 방법
데이터의 차원수, 갯수가 많아질수록 사람의 육안만으로 데이터를 몇개의 그룹으로 군집화해야겠다는 감을 잡기가 어렵다. 그래서 수학적으로 몇 개의 그룹으로 데이터를 묶어줘야하는지 계산해야한다.
각 cluster의 중심점, 거리 차이의 분산(inertia)를 최소화하는 방식으로 동작
- Inertia : 각 클러스터 별 오차의 제곱합(분산)
- 각 데이터로부터 자신이 속한 군집의 중심까지의 거리
- inertia가 낮을수록, 군집화가 더 잘됐다.
- inertia가 급격하게 변하는 지점을 최적의 k로 설정
see = {}
for k in range(1,10): # cluster 1~9
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans.fit(rfm_scaled) # scaling된 rfm값
see[k] = kmeans.inertia_
sns.pointplot(x=list(see.keys()), y=list(see.values()))
EDA
- 데이터 정제
- Feature Engineering
- RFM 지표에 관한 새 Feature 생성해보자
- RFM
- Recency : 고객의 마지막 구매 시점
- 최근에 구매한 고객일수록 현재의 관계에 유의하다.
- Frequency : 구매 빈도
- 고객의 구매, 이용 활동성 판단 가능
- 수요가 있는 품목 위주로 마케팅 전략 세우기
- Monetary : 얼마나 많이 소비했는가?
- 지나치게 높은 구매액 존재 시, 상한선을 두어 전체적인 지수 왜곡 방지 가능
- RFM data 합치기
rfm = rfm_r.join([rfm_f, rfm_m], how='inner')
- (https://exchange.tableau.com/ko-KR/products/531)
- Recency : 고객의 마지막 구매 시점
- Log Transformation
- 치우쳐져 있는 분포를 학습하면, 골고루 학습하지 못하여 부정확한 결과를 반영한다.
- 예측 변수, 목표 변수가 정규 분포를 따를 때 더 신뢰할 수 있는 예측이 이루어진다.
- log transformation 시행 전에, value가 0인 데이터 삭제해줘야함.
- 치우쳐져잇는 분포 → log transformatiaon → 정규분포와 비슷한 모양의 분포를 갖게함
- cf) 표준화는 분포의 모양 자체를 바꾸지 않고 평균을 0인 곳으로 옮겨주는 것이므로 헷갈리지 말기
# RFM의 Frequency를 예로 살펴보자.
sns.displot(rfm['Frequency'])

frequency_log = np.log(rfm['Frequency'])
sns.displot(frequency_log)
- Data Scaling
# StandardScaler : mean을 0, std를 1로 normalize함.
scaler = StandardScaler()
rfm_scaled = scaler.fit_transform(log_rfm)Build Clustering Model
앞서 보았던, Elbow Method를 이용해 최적의 k값을 구하고, K-Means Clustering 진행하자.
# Elbow Method를 통해 최적의 k값이 3이 나왔다고 해보자.
# 최종 모델 학습
kmeans = KMeans(n_clusters=3, max_iter=50, random_state=42)
kmeans.fit(rfm_scaled)
# 각 고객이 속한 클러스터 label 확인
cluster_labels = kmeans.labels_
# assign함수를 사용해, 'rfm'데이터 프레임에 'Cluster'열 추가해 각 고객의 클러스터 레이블 할당
rfm_k3 = rfm.assign(Cluster = cluster_labels)
# df.assign(new_column=values)
# df에 새로운 열 'new_column'이 추가되고, 해 열의 값은 values이다.# 예를 들어, 각 Cluster(0,1,2)별로 고객들의 Frequency값의 분를 살펴보자.
var = [cluster_0.Frequency, cluster_1.Frequency, cluster_2.Frequency]
cluster = ['cluster 0', 'cluster 1', 'cluster 2']
fig, ax = plt.subplots(3,1, figsize=[8,8]) # 3개의 subplot을 가지는 1개의 그래프 생성
for i in range(len(var)):
variable = var[i]
ax[i].hist(variable, alpha=0.5)
ax[i].set_xlim(0, var[i].max())
ax[i].set_xlabel(f'{cluster[i]}')
ax[i].set_title('Frequency')
plt.subplots_adjust(hspace=0.8) # hspace : 각 subplot들의 수직간격 설정
# suplots_adjust : subplot 간의 간격 조정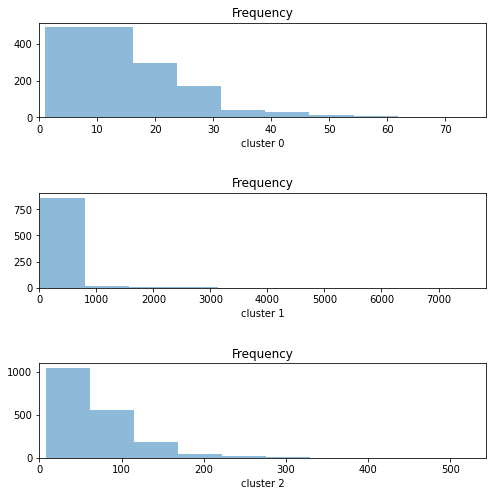
RFM의 각 데이터를 3D 산점도를 사용해 시각화해보자!
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(13,10))
ax = fig.add_subplot(111, projection='3d') # 3d subplot 생성
# 111 : 1x1크기의 subplot 생성, 첫번째 위치에 배치하도록 지정
ax.scatter(xs=rfm_k3.Recency, ys=rfm_k3.Frequency, zs=rfm_k3.Monetary, c=rfm_k3.Cluster)
# ax.scatter(xs, ys, zs, c=cluster별 datapoint의 다른 색상부여)
# Recency, Frequency, Monetary 값을 각각 x,y,z축으로 하는 3차원 산점도 생성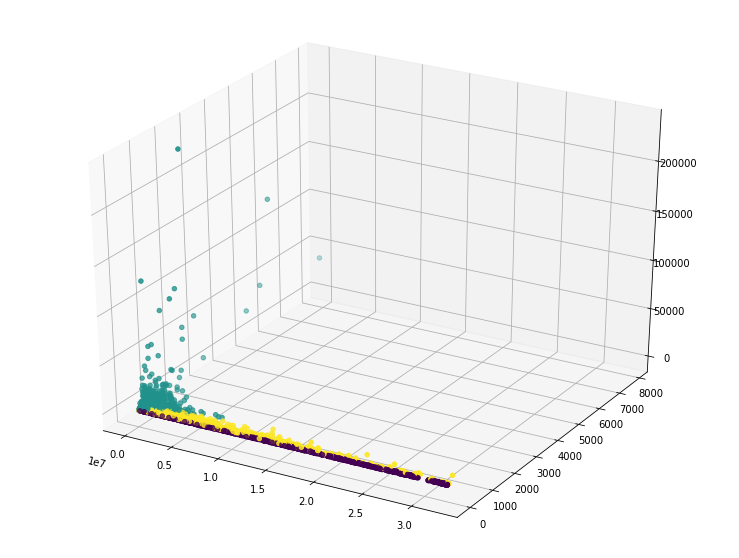
클러스터별 특징 분석
Cluster별 특징 분석을 통해, 사용자의 특성별로 각기 다른 정책을 적용하고 서비스를 더 잘 사용하게끔 유도하는 전략을 세워볼 수 있다.
cluster_avg = rfm_k3.groupby(['Cluster']).mean()
population_avg = rfm.mean()
# 상대적인 중요도 계산
relative_imp = cluster_avg / poplutaion_avg
# heatmap을 통해 각 Cluster의 Recency, Frequency, Monetary가 전체 population에 얼만큼 차지하는가를 통해 중요도 확
sns.heatmap(relative_imp, annot=True, fmt='.2f', cmap='RdYIGn')
# annot=True : 각 셀에 숫자 표시
# cmap='RdYIGn' : 색상맵 지정, 양수:빨강, 음수:녹
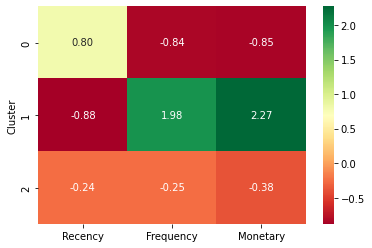
→ Cluster 1 소비자 그룹은 전체 population의 구매 빈도수, 소비량에 많은 부분 차지하고 있어, 그룹의 소비자들이 구매 빈도수와 구매량을 계속 유지하는 것이 회사 입장에서 중요한 부분일 것임.
More Study
Silhouette Score
( elbow method로 사용하기 어려울때)
- elbow method와 같이, 모두 clustering에서 최적의 k를 결정하는데 사용
- clustering의 품질 측정
- clustering 결과를 각 datapoint의 silhoutte coefficient를 계산해 평균값을 구하고, 이 값이 클수록 clustering 결과가 좋다고 판단
- 평균 silhouette coefficient : -1~1
- 1에 가까울수록 자신이 속한 cluster과 다른 cluster과의 거리가 멀리 떨어져있음
- -1에 가까울수록, 샘플이 잘못된 cluster에 속해 있음
- 0에 가까울수록, 샘플이 속한 cluster과 다른 cluster과의 거리가 비슷하다.
- 각 datapoint의 silhouette coefficient는 해당 datapoint가 속한다른 cluster들과의 거리를 기반으로 계산됨.
- elbow method는 비교적 간단하게 적합도를 시각화하여 최적의 cluster개수를 결정하는 반면, silhouette 분석은 더 정교한 방법으로 clustering 결과의 품질을 측정하고, 이를 통해 최적의 cluster개수를 결정함.
from sklearn.metrics import silhouette_score
silhouette_scores = []
for i in range(2,11): # cluster 2~10
kmeans = KMeans(n_clusters=i, max_iter=50, random_state=42)
kmeans.fit(rfm_scaled)
cluster_labels = kmeans.labels_
silhouette_avg = silhouette_score(rfm_scaled, cluster_labels)
# silhouette_score(군집화수행한 dataset, cluster label)
# 각 샘플의 실루엣 계수를 계산해, 평균 실루엣 계수 반환
silhouette_scores.append(silhouette_avg) # silhouette coefficient를 리스트에 저장
# 저장된 silhouette coefficient 그래프로 시각화
plt.plot(range(2,11), silhouette_scores, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.show()
print(silhouette_scores)
>> [0.3991089517098286, 0.311345789466801, 0.2967959321783024, 0.2831345274398782, 0.2626769762664394,
0.2720101110427263, 0.26756437315771175, 0.2571228916547968, 0.2616553270658572]
# 실루엣 계수가 가장 높은 cluster 개수를 찾아 최적의 k 구하기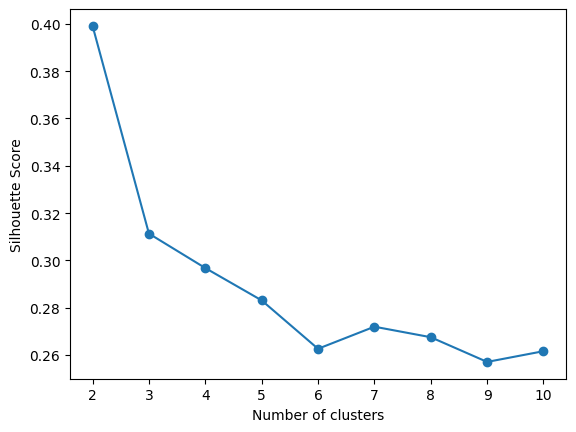
Kmeans clustering with Elbow Method and Silhouette
Explore and run machine learning code with Kaggle Notebooks | Using data from Mall Customer Segmentation Data
www.kaggle.com
hierarchical clustering
- 모두 대표적인 Clustering 알고리즘
- clustering 결과를 dendrogram으로 나타낸다.
- 먼저 모든 datapoint를 개별 cluster로 보고, 가장 가까운 cluster끼리 하나의 cluster로 합쳐나감.
- 합치는 방법에 따라 Agglomerative Clustering, Divisive Clustering으로 나뉨.
- Agglomerative Clustering : 가장 가까운 두 cluster 합치는 방법(bottom-up방식)
- Divisive Clustering : cluster를 둘 이상으로 나누어가는 방법(up-bottom 방식)
- K-means clustering은 cluster의 개수를 미리 지정해야하며, clustering한 결과가 non-overlapping하며, 전체 dataset을 기준으로 clustering됨.
- 반면, Hierarchical clustering은 cluster개수를 미리 지정하지 않아도 되며, clustering결과가 overlapping할 수 있으며 계층 구조를 가짐. and dendrogram을 이용해 시각화할 수 있어, clustering 결과를 해석하기 더 용이하다.
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
# feature만 추출 (cluster열만 빼고 추출)
X = df.iloc[:,:-1]
# Hierarchical Clustering (Agglomerative 군집화 방법 사용)
hc = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
# affinity : 거리 측정 방법, linkage:클러스터 간 거리 측정 방법
hc.fit(X)
# dendrogram 시각화
linked = linkage(X, 'ward')
# linkage : 각 cluter를 결합하는 방법으로, cluster간의 거리 측정하고, 어떤 거리 척도를 기준으로 cluster결합할 것인지 결
# ward:linkage 방법 중 하나. 'ward'방법은 분산을 최소화하는 것이 목적이며, 일반적으로 잘 작동함
dendrogram(linked)

최적의 k를 찾는 또 다른 방법으로는, dendrogram에 수직선을 그리면서, 수평선과 dendrogram이 만나는 거리가 급격하게 커지는 부분을 찾아 최적의 cluster개수 결정 가능. 이 지점에서 군집 간 거리가 늘어나면서, 군집 내 분산이 줄어들어 최적의 군집 개수를 찾는것임.
- hierarchical clustering에서 미리 cluster 개수를 지정하지 않아도 된다고 했는데, 위 코드인 hierarchical clustering의 일부인 agglomerative clustering에서는 미리 cluster개수를 지정했다. 미리 cluster개수를 지정해도 되고 안해도 된다고 한다.
- cluster개수를 미리 지정하지 않을 시 : n_clusters대신, n_clusters=None, distance_threshold=5파라미터를 사용하여 거리의 임계값을 지정해준다. 이 거리보다 작은 값은 하나의 cluster로 간주하며 수행.
- cluster=None, distance_threshold=10으로 해보았는데, hc_label에 들어있는 값들이 매우 크게 나와서 이상한가 했는데, 결국 dendrogram을 그려보니, cluster를 미리 지정했을 때와 똑같은 결과가 나왔음. and distance_threshold를 크게할수록 hc_label의 값들은 작아짐. cluster미리 지정했을 때와 안했을 때의 dendrogam은 비슷하다는 결과가 나옴.
- K-means clustering의 단계 시각적 확인
initial centroid, 데이터 분포 선택해 Add Centroid를 통해 중심점 추가하거나, Go!를 클릭해 K-menas clustering 시작!
Update Centroids, Reassign Points를 통해, clustering 과정 시각적으로 살펴보자!
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
Visualizing K-Means Clustering
January 19, 2014 Suppose you plotted the screen width and height of all the devices accessing this website. You'd probably find that the points form three clumps: one clump with small dimensions, (smartphones), one with moderate dimensions, (tablets), and
www.naftaliharris.com
- 어제 배운 차원 축소 기법을 어떻게 적용할 수 있을까?
- PCA는 K-means Clustering과 함께 사용될 때, 고차원 데이터에서 중요한 변수만 추출해 Clustering을 수행할 수 있다. 예를 들어, RFM 데이터를 Clustering할 때, PCA를 적용하면 Recency, Frequency, Monetary 등의 변수를 고차원에서 저차원으로 축소하여 Clustering을 수행하여, 더 나은 Clustering 결과를 얻을 수 있다.
