- ridge regression을 통해 bias를 약간 높이게 되면, 어떤 효과를 얻나?overfitting시, bias는 작고, var은 높다. 이를규제 모델인 ridge에서 alpha 매개변수를 증가시켜, bias를 높여 일반화 성능을 향상시킨다.
- overfitting 해결
- 람다(penalty)값을 크게 잡으면 어떤 효과가 있나?alpha가 크면, 모델의 가중치 값이 작아지는 경향이 있어, 모델의 복잡도를 낮출 수 있다.
- Ridge회귀에서 alpha 값이 크면, 가중치 계수가 작아진다.
- Lasso회귀에서 alpha 값이 크면, 일부 가중치 계수가 0으로 수렴할 수 있다.
- lambda = penalty = alpha (같은 의미로 보면 된다)
과적합을 어떻게 방지할 수 있을까?
1. 더 많은 데이터 학습시키기
2. 특성 수 줄이기
3. 규제 모델 사용
- 모델에 규제항을 더해 기존 모델보다 단순하게 만듬
- 규제항(alpha) : 회귀계수 값이 너무 커지는 것을 방지해줌
- 선형모델이 학습데이터에 덜 적합하게 만들고, 일반화 성능을 높이는 역할
🌀 Regularized Regression
회귀분석 용어 정리

- SSE : Sum of Squares Error (잔차 제곱합) = RSS (Residual Sum of Squares) : 실제값, 예측값 차이 제곱합
- SSR : Sum of Squares Regression (회귀 제곱합) : 예측값, 평균값 차이 제곱합
- SST : Sum of Squares Total (잔차 제곱합) = SSE + SSR : 실제값, 평균값 제곱

회귀는 SSE를 최소화하는 직선을 긋는 것
SSE\n = MSE → root ⇒ RMSE ( SSE가 최소화가 되면 RMSE도 최소화가 되겠지 )
Ridge Regression
(L2 penalty) : 가중치들의 제곱합
영향력이 크지 않은 회귀계수 값을 0에 가까운 수로 (0은 아님.)

Lasso Regression
(L1 penalty) : 가중치들의 절대값의 합
영향력이 크지 않은 회귀계수 값을 0으로 만든다.
sparse model : 가중치가 0인 특성이 많은 모델
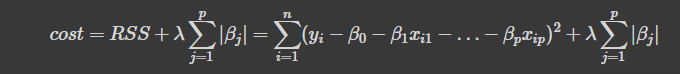
λ (alpha)
alpha = lambda = penalty term = regularization term
alpha값이 클수록, 회귀계수 값이 줄어든다. → 가중치를 줄여줌으로써, 일반화 성능 올리기
λ=0 인 경우, 기존의 선형회귀와 같아진다. (기준모델로 평균모델 삼을때 r2 생각)

첫번째 그래프 : Lasso Regression
- L1 penatly로, 회귀계수의 절대값이기 때문에 회귀계수가 움직일 수 있는 공간이 마름모꼴
두번째 그래프 : Ridge Regression
- L2 penalty로, 회귀계수의 제곱이기 때문에 회귀계수가 움직일 수 있는 공간이 원형
→ Lasso Regression은 영향력이 작은 회귀계수의 값이 마름모의 제일 위인 0이 되고, Ridge Regression은 0에 가까운 수로 축소한다.
scikit-learn이용해 ridge, lasso Regression 구현
OLS(선형회귀) vs Ridge vs Lasso

Scaling & Encoding
정규화모델은 특성의 스케일을 표준화하는 것이 필요
Scaling ( 수치형 변수 스케일링)
StandardScaler 사용
(train data) fit_transfrom : 먼저 변환할 규칙을 찾아줌
(test data) transform : 규칙을 찾아주었으니, 변환을 해줌
- mean=0에, std=1에 가깝게 변환해줌
Encoding : 문자형→숫자형
- One-hot-Encoding
x = df.drop('SalePrice', axis=1)
y = df['SalePrice']
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2, random_state=42)
# 수치형 변수만 Scaling
numeric_feats = x_train.dtypes[x_train.dtypes!='object'].index
scaler = StandardScaler()
x_train[numeric_feats] = scaler.fit_transform(x_train[numeric_feats])
x_test[numeric_feats] = scaler.transform(x_test[numeric_feats])
# One-hot-Encoding
# 범주형 변수들이 0,1 값을 가지게 모두 수치적 표현됨.
ohe = OneHotEncoder()
x_train = ohe.fit_transform(x_train)
x_test = ohe.transform(x_test)
# category_mapping 메소드 사용시, 범주형 특성이 어떻게 변환되었는지 확인 가능
ohe.category_mapping
>> [{'col': 'MSZoning', 'mapping': RL 1
FV 2
RH 3
RM 4
C (all) 5
NaN -2
dtype: int64, 'data_type': dtype('O')},
{'col': 'Street', 'mapping': Pave 1
Grvl 2
NaN -2
dtype: int64, 'data_type': dtype('O')},.....모델 학습 시작해보자!
기준, 다중선형회귀, Ridge선형회귀, Lasso선형회귀, Elastic 선형회귀 총 5개를 훈련, 검증 모델을 비교하며 성능 측정하자! 성능이 가장 좋은 모델을 최종 모델로 선정하자. 최종 모델을 이용해 테스트셋에 넣어 최종 성능을 예측해보자.
Feature Selection - selectKBest 사용
- 주어진 score function에 따라 가장 높은 점수를 가진 k개의 특성만 선택
- 주어진 score function에서, 각 특성과 타겟 변수 간의 선형 관계를 평가하고, 가장 높은 F-value를 가진 k개의 특성 선택
- F-value : ANOVA(Analysis of Variance) 에서 사용되는 값으로, 독립 변수와 종속 변수 사이의 분산 비율을 나타낸다.
- 이 비율이 클수록, 독립 변수가 종속 변수에 미치는 영향이 크다.
- score_funciton = ‘f_regression’ : F-value을 계산하는 함수 중 하나
# 기준 모델 : 평균 사용 (모델 예측의 하한선)
base = [y_train.mean()] * len(y_train)
base_r2 = r2_score(y_train, base)
base_mae = mean_absolute_error(y_train, base)
>> 기준모델의 r2 score: 0.0
>> 기준모델의 MAE score: 65.17387978949326
# 모델 성능 평가 함수
def print_score(model, x_train, y_train, x_test, y_test):
# model.score 사용시, predict 안하고 사용 가능
# r2_score 사용시, predict 후 사용 가능
train_score = model.score(x_train, y_train)
val_score = model.score(x_val, y_val)
test_score = model.score(x_test, y_test)
return train_score, val_score, test_score
# 다중 선형회귀 (OLS)
ols = LinearRegression()
ols.fit(x_train, y_train)
print_score(ols, x_train, y_train, x_test, y_test)
>> 학습 세트 r2_score : 0.929
검증 세트 r2_score : -5.174993524076134e+19
테스트 세트 r2_score : -4295694290873353.5
(전혀 예측을 못하네..)
# 다중 선형회귀 - Feature Selection
# 어떻게 하면 효과적으로 예측에 유용한 특성을 선택할 수 있을까?
# 주어진 score_func에서 가장 높은 점수를 가진 50개 특성만 뽑아서 과적합을 막을수있나 보자.
selector = SelectKBest(score_func=f_regression, k=50)
x_train_selected = selector.fit_transform(x_train, y_train)
x_test_selected = selector.transform(x_test)
# 어떤 특성이 선택되었는지 확인
selector.get_feature_naems_out()
>> array(['MSZoning_4', 'LotFrontage', 'Neighborhood_1', 'OverallQual',
'Exterior1st_1', 'Exterior2nd_1', 'MasVnrType_1', 'MasVnrType_2',
'MasVnrArea', 'ExterQual_1', 'ExterQual_2', 'ExterQual_3',
'Foundation_1', 'Foundation_2', 'BsmtQual_1', 'BsmtQual_2',.....
# Feature Selection된 다중 선형회귀 모델
ols_fs = LinearRegression()
ols_fs.fit(x_train_selected, y_train)
print_score(ols_score, x_train_selected, y_train, x_test_selected, y_test)
>> 학습 세트 r2_score : 0.828
검증 세트 r2_score : 0.784
테스트 세트 r2_score : 0.848→ train set는 성능이 조금 떨어졌지만, test set을 보면, 과적합이 해소된 것을 볼 수 있다.
→ (Feature Selection - SelectKBest)총 282개의 feature 중 50개만 사용해도, 충분히 예측이 가능하다는 사실 알았다.
본격적으로, 규제 모델 사용해보자!
alpha값이 커질수록, 회귀계수가 작아지고, 모델의 성능도 변한다.
이 alpha값을 보다 효율적으로 구할 수 있는 방법 : RidgeCV, lassoCV
Ridge Regression
# Ridgecv 학습
alphas = np.arange(1,100,10)
ridge = RidgeCV(alphas=alphas, cv=5)
ridge.fit(x_train, y_train)
# 최적의 alpha값
ridge.alpha_
print_score(ridge, x_train, y_train, x_val, y_val)
>> alpha: 11
train r2 score : 0.551851499727552
val r2 score : 0.49453047998856925
train MAE score : 34.06115252644997
val MAE score : 35.649847514064454만약, 많은 특성 중 예측에 쓰이는 특성이 몇개 뿐이라고 의심될 때는 불필요한 특성의 회귀계수를 0으로 만들어, 확실한 특성선택의 효과를 가져오는 Lasso가 좋은 성능을 보일 수도 있다. (Feature의 개수가 매우 많은 경우 사용하기에 적합할듯!)
Lasso Regression
# Lassocv 학습
alphas = np.arnage(10,200,10)
lasso = LassoCV(alphas=alphas, cv=5)
lasso.fit(x_train, y_train)
lasso.alpha_
print_score(lasso, x_train, y_train, x_val, y_val)
>> alpha: 10
train r2 score : 0.3446716274271787
val r2 score : 0.3819850756550732
train MAE score : 43.63118731546043
val MAE score : 43.16827666498575
pd.Series(lasso.coef_, x_train.columns).sort_values(ascending=False).head(10)
>> total_sqft 44.514894
bath 31.101458
area_type_1 -0.000000
location_706 -0.000000
location_713 0.000000
location_712 -0.000000
location_711 0.000000
location_710 0.000000
location_709 -0.000000
location_708 -0.000000
# 이처럼 lasso는 회귀계수가 0까지 수렴하게 해줌.- OLS, Ridge, Lasso 회귀 계수 비교

OLS에 비해, 정규화 모델의 회귀계수의 값이 많이 줄어들었다.
이처럼, 정규화 모델은 정규화를 통해 특이값으로 인한 과도한 기울기를 보정해준다.
정규화 모델은 몇몇 중요한 특성들만 회귀계수가 크고, 대부분 0근처에 있다.
→ 영향력이 낮은 특성의 회귀계수값을 감소시켜 특성선택의 효과를 가져온다. (특히 Lasso의 경우 중요하지 않은 특성의 회귀계수가 0으로 변환된 것 확인)
ElasticNet Regression
= Ridge(L2), Lasso(L1) penalty를 모두 사용하는 정규화 모델
각자의 장점을 결합해, 모델의 가중치를 작게 만들면서도, feature selection을 수행할 수 있다.
alphas = np.logspace(-5,2,8)
elas = ElasticNetCV(alphas=alphas, cv=5)
elas.fit(x_train, y_train)
enet.alpha_
print_score(enet, x_train, x_val, y_train, y_val)→ 지금까지 한 것 중 최종 모델 선택해 일반화능력을 높여보자~
모델에 따라 각각의 장단점이 있으며,
각 데이터셋, 모델의 특성에 따라 어떤 방법을 사용할지 결정하는 것이 중요!
More Study
# 소수점 이하 4자리까지 출력하도록 설정
pd.set_option('display.float_format', lambda x: f'{x:.4f}')다중공선성 (multicollinearity)
: 회귀 분석에서 독립 변수들 간에 강한 선형 관계가 있을 때 발생
- 독립변수들 간 상호상관관계가 강한 경우 발생
- 이는, 독립변수의 공분산 행렬이 full rank이어야 한다는 조건 침해
- overfitting 발생하기 쉽다.
다중공산성 해결 방법
가장 기본적인 방법으로는, 다른 독립변수에 의존하는 변수를 없애는 것.
가장 의존적인 독립변수 선택하는 방법 : VIF (Variance Inflation Factor)
VIF
- 독립변수를 다른 독립변수로 선형회귀한 성능
- 다른 변수에 의존적일수록, VIF가 커진다.

from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = [variance_inflation_factor(df.values, i) for i in range(df.shape[1])]⇒ 다중공산성 제거후, overfitting 완화, 일반화 능력 good해질 수 있다.
Multicollinearity in Multiple Linear Regression
https://medium.com/analytics-vidhya/multicollinearity-in-multiple-linear-regression-e23997406c70
[Reference]
- StatQuest video on Ridge Regression:
- ridge regression을 통해서 bias를 약간 높이게 되면 어떤 효과를 얻게 되나요?
- 람다(패널티) 값을 크게 잡으면 어떤 효과가 있나요?
- StatQuest video on Lasso Regression:
- ridge regression과 lasso regression의 차이는 무엇인가요?
- Regularization: Ridge Regression and the LASSO
- 이 패널티값을 보다 효율적으로 구할 수 있는 방법이 있을까요?
So how do we decide what value to give lambda? We just try a bunch of values for lambda, and use cross-validation
도서
- The Elements of Statistical Learning
- Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow
'Machine Learning' 카테고리의 다른 글
| [The Based Models 2] Boosting (0) | 2023.04.14 |
|---|---|
| [The Based Models 1] Tree Based Model (0) | 2023.04.14 |
| [Linear Models 4] Logistic Regression (0) | 2023.04.14 |
| [Linear Models 2] Generalization (0) | 2023.04.14 |
| [Linear Models 1] Linear Regression (0) | 2023.04.14 |
