Logistic Regression은 Classification 문제이다.
지도 학습은 회귀 문제 / 분류 문제로 나눌 수 있다. 회귀 문제, 분류 문제는 어떤 차이점이 있나?
| Regression | Classification | |
|---|---|---|
| target 변수 형태 | 연속적인 값 | 이산적인 값(class label) |
| 모델 학습 방법 | 예측값, 실제값 차이 최소화 | 분류 결과의 정확도 최대화 |
먼저 문제상황을 보고, 분류 문제인지 회귀 문제인지 아는 것 중요!

🌀 Classification 문제
분류 문제는 데이터가 속할 특정 범주 (특정 범주에 속할 확률) 예측
기준모델 : 보통 최빈 클래스로 설정
타겟 범주가 편중된 비율을 가질 경우가 많다.
타겟값의 비율이 class0 : class1 = 1:9인 데이터를 가지고 모델을 만들었는데, 예측 정확도가 90%가 나왔다. 이 모델은 좋은 모델일까?→ x. 위의 모델은 모든 데이터를 class1으로만 예측해도 예측 정확도 90% 달성 가능!
이런 경우, 최빈클래스 기준의 기준모델의 예측 정확도 90%를 기준으로 이보다 더 좋은 성능을 가진 모델을 만들기 위해 노력해야함!
Logistic Regression
선형회귀로 분류 문제를 풀 수 있을까?
선형회귀의 결과값은 -∞ ~ +∞이다. 이와 같은 결과값으로는 어떤 특정 범주에 속할 확률을 정확하게 알 수 없다.
But, 선형회귀 + 시그모이드 함수 → 로지스틱 회귀 → 확률을 구할 수 있다!
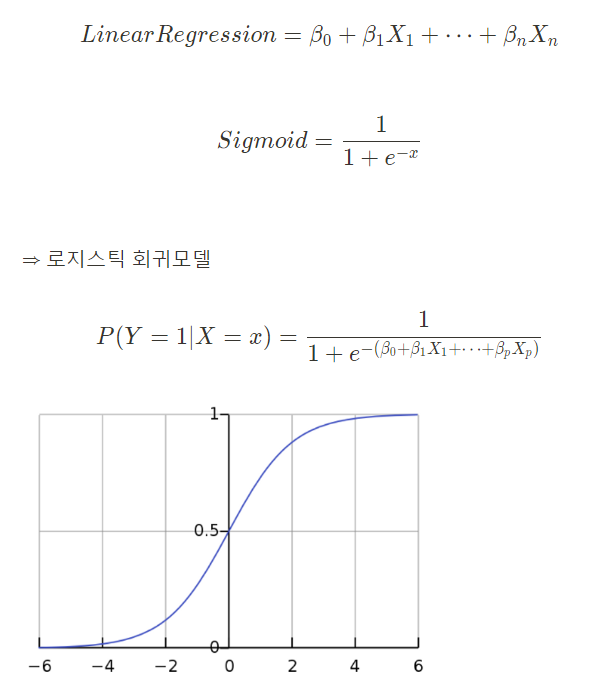

왜 로지스틱 회귀에서 sigmoid함수를 사용하는가?
사건 안발생(0), 사건 발생(1)의 결과를 선형으로 표현했을 때 문제점이 발생하기 때문이다.

x의 값이 대략 6인 지점을 기준으로, 6보다 작으면 사건 안발생(0), 6보다 크면 사건 발생(1)이다.
But, x의 값이 9일때, 사건 안발생(0)으로 예측이 틀리게 된다.
⇒ 새로운 값의 추가가 기존 분류 모델에 큰 영향을 미치게 되는 문제점 발생
이런 문제점을 해결하기 위해, 그래프를 직선으로 표현하는 것 대신, 완만한 S자형 곡선으로 나타내어, 위와같은 문제점을 완화시킨다.
분류 문제를 풀기 전에, 항상 먼저 타겟의 범주가 어떤 비율을 가지고 있는지 확인해야함 !
(불균형함을 알아보기 위해)
🌀 Classification 평가 지표
Confusion Matrix

예측이 맞을 때 : P / 예측이 틀릴 때 : N
예측값이 실제로 맞을 때 : T / 예측값이 실제로 틀릴 때 : F
Precision, Recall
| 예측 0 | 예측 1 | |
|---|---|---|
| 실제 0 | TN | FP |
| 실제 1 | FN | TP |

타겟이 불균형한 경우 , Accuracy는 모델의 성능을 비교하기 어려움.
- Precision(정밀도) : 1이라 예측한 것 중 진짜 1인것 (예측 관점)
- Recall(=Sensitivity, 재현율) :실제 1인 것을 1이라 예측한 것 (실제 관점)
recall이 낮으면, 암환자한테 암이아니라고 하는것 (인간의 목숨이 왔다갔다하는 것 = 민감도)
왜 1(positive)만 따지나 ? 양성이 중요한 것이니까. (물론 때로는 0이 중요할 때도 있으나, 양성이 더 중요!)
precision, recall은 각각 관점이 다르므로, 이 둘의 조화평균 = f1-score
다루는 문제에 따라 precision, recall 중 어느 평가지표를 우선시 해야하는지 판단해야함!
어떤 에러가 더 치명적인지 봐야함!
precision : FP가 더 치명적이라 생각할때 (암아닌 사람을 암이라고 예측)
recall : FN이 더 치명적이라 생각될때 (암인 사람을 암이 아니라고 예측)
→ 암 예측시, FN이 더 치명적인 오류일 것이다. → 이 경우, Recall이 Precision보다 더 중요!
cf) 또 다른 예로는, 일반적으로, 스팸 메일 분류 모델에서는 Recall보다는 Precision을 사용한다. (스팸메일이 아닌 것을 스팸메일이라고 예측시 치명적→ 스팸 메일을 놓치면, 중요한 메일을 놓칠 수 있으므로, FP가 더 치명적이니까)
현재 모델에서 recall 값을 더 올릴 수 있을까?
→ 임계값에 따라 1로 분류 / 0으로 분류되는 샘플의 개수가 달라진다.
임계값을 낮추면, recall이 늘고, precision이 주는 것 확인 가능
Precision-Recall Trade-Off
임계값이 커지면 모델 positive라고 예측하는 샘플의 수가 적어진다.
- Positive인데, negative라고 예측하는 비율 높아짐.
- → FN 증가 ⇒ recall 감소
- Positive라고 예측하면, 실제 positive인 비율 높아짐
- → FP 감소 ⇒ precision 증가
임계값이 작아지면 모델이 positive라고 예측하는 샘플의 수 많아짐.
- Negative라고 예측하면, 실제 negative인 비율 높아짐.
- → FN 감소 ⇒ Recall 증가
- Negative인데, positive라고 예측하는 비율 높아짐.
- → FP 증가⇒ Precision 감소
precision, recall은 trade-off 관계이므로, 최적의 임계값을 두고 푸는 것이 중요하겠지!
accuracy score만이 높다고 해서 좋은 성능이 아니다.
하지만, 현업에서는 recall이 더 중요하게 쓰이므로 recall이 얼마인지도 고려해야한다!
위는 모델이 예측한 이후, 분류한 샘플의 수를 가지고 성능을 측정했다.
모델의 예측값 자체를 평가하는 지표를 살펴보자.
ROC, AUC
(Reciever Operating Characteristic, Area Under the Curve)
: 모델이 예측하는 확률을 평가하는 지표

ROC Curve
임계값을 변화하면서 TPR, FPR 비율을 그래프로 나타낸 것
재현율을 높이기 위해서는 Positive로 판단하는 임계값을 계속 낮추어 모두 Positive로 판단하게 만들면 된다. 하지만 이렇게 하면 동시에 Negative이지만 Positive로 판단하는 위양성률도 같이 높아진다.
- 임계값이 1인 경우, TPR=FPR=0
- 임계값이 0인 경우, TPR=FPR=1
아래 링크에서 두 클래스의 분포와 임계값을 변형시키며 ROC Curve의 변화 살펴보기 Understanding ROC Curve
→ TPR 최대, FPR 최소가 되는 최적의 임계값 찾아, recall을 올려보자!
AUC
ROC 곡선 아래의 면적을 이용해, 분류 모델의 성능을 나타냄
일반적으로, AUC가 1에 가까울수록 좋은 성능, 0.5에 가까울수록 안 좋은 성능 모델임.
AUC score : 모델이 class 1샘플의 예측값을 class 0샘플의 예측값보다 크게 줄 확률
분류 결과보다, 모델의 예측값 자체(확률 자체)가 중요한 경우 많이 사용됨.
ex) 영화 추천 모델(각 영화에 대해 유저가 볼 것인가 보지 않을 것인가를 분류하는 경우), 일반적으로 모델의 예측 점수에 따라 웹 사이트에서 영화 제시 (모델의 예측확률이 높은 순서대로 영화 제시하겠지!!)




Modeling
통신사 고객의 계약 해지 데이터셋인 Telco Customer Churn 를 사용해서 해지 여부를 예측하는 분류 문제를 풀어보자!
target feature : ‘Churn’
# 분류문제에서는, 먼저 타겟 값 분포를 확인해야함! (불분명할수도 있기 때문)
df['Churn'].value_counts(normlize=True).plot(kind='bar')
>> No 0.735508
Yes 0.264492
x = df.drop('Churn', axis=1)
y = df['Churn']
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2, stratify=y, random_state=42)
# stratify=y : 타겟데이터 불균형 시 거의 필수적!
# 각 분할에서의 타겟 값의 분포가 전체 데이터 집합에서의 타겟값의 분포와 거의 동일
# Scaling
# 수치형 특성
num_feats = x_train.dyptes[x_train.dtypes!='object'].index
scaler = StandardScaler()
x_train[num_feats] = scaler.fit_transform(x_train[num_feats])
x_test[num_feats] = scaler.transform(x_test[num_feats])
# Encoding
# 범주형 특성
ohe = OneHotEncoder(use_cat_names=True)
# use_cat_names : 변환된 변수의 이름에 범주형 변수의 이름을 사용하도록 지정
# 변환된 변수의 이름이 의미를 파악하기 쉽고 해석이 용이타겟 분포 불균형한 경우
- train_test split 시,stratify=y사용
- logistic regression 시,class_weight=’balanced’
→ 사용하냐안하냐에 따라, 성능 차이 꽤 크다.
# 기준 모델 : 최빈값 이용
base = [y_train.mode()[0]] * len(y_train)
accuracy_score(y_train, base)
>> base accuracy: 0.7355# 로지스틱 회귀 모델
model = LogisticRegression(class_weight='balanced')
# 타겟 클래스의 비율이 불균형하므로 class_weight='balanced' 사용
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
model.score(x_train, y_train)
model.score(x_test, y_test) # = accuracy_score(y_test, y_pred)
recall_score(y_test, y_pred)
>>
학습 Accuracy 0.7516
평가 Accuracy: 0.7409
평가 Recall: 0.7795
# 확률값 확인
model.predict_proba(x_test)[:5] # default : thresholds=0.5 기준!
>> [[0.11207934 0.88792066] # 1
[0.18564831 0.81435169] # 1
[0.48079965 0.51920035] # 1
[0.86450991 0.13549009] # 0
[0.96940387 0.03059613]] # 0
# 0,1 중 확률값이 큰 값의 인덱스가 예측된 결과로 사용!
model.predict_proba(x_test)[:5].argmax(axis=1)
>> [1 1 1 0 0]
# 회귀계수 해석
coef = pd.DataFrame()
coef['feature'] = model.feature_names_in_
coef['coefficient'] = model.coef_.reshape(-1,1)
coef.sort_values(by='coefficient', ascending=False, inplace=True)
coef.reset_index(drop=True, inplace=True)
# 상위 3개
coef.head(3)
>> feature coefficient
0 Contract_Month-to-month 0.7120
1 InternetService_Fiber optic 0.6816
2 TotalCharges 0.6154
# 이 column들은 타겟 값에 영향을 많이 끼치겠지.로지스틱 회귀모델의 회귀계수가 양수라면, 해당 특성의 값이 커질 때 1의 클래스에 속할 확률이 커지고,
회귀계수가 음수라면 해당 특성의 값이 커질 때 1의 클래스에 속할 확률이 줄어든다.
⇒ 회귀계수의 절대값이 클수록 영향력이 크다.
cf) 만약, threshold를 0.5말고, 따로 지정해주고 싶다면, 수동 지정!
threshold = 0.7
y_test_proba = model.predict_proba(x_test)
# 예측 결과를 0,1 class로 변환
pred = np.where(y_test_proba[:,1] > threshold, 1,0)
# 0.7보다 크면 1로 분류
# 0.7보다 작으면 0으로 분류
from sklearn.metrics import plot_confusion_matrix
fig, ax = plt.subplots()
pcm = plot_confusion_matrix(model, x_test, y_test, cmap='Blues', ax=ax)
from sklearn.metrics import classification_report
# 분류 평가 지표 - 로지스틱 회귀 분류 모델
classification_report(y_test, y_pred)
>> precision recall f1-score support
0 0.90 0.73 0.80 1033
1 0.51 0.78 0.61 372
accuracy 0.74 1405
macro avg 0.70 0.75 0.71 1405
weighted avg 0.80 0.74 0.75 1405
# 분류 평가 지표 - 기준 모델(최빈값)
classification_report(y_test, base, zero_division=True)
# zero_division : 분모가 0인 경우 어떻게 처리할지
>> precision recall f1-score support
0 0.74 1.00 0.85 1033
1 1.00 0.00 0.00 372
accuracy 0.74 1405
macro avg 0.87 0.50 0.42 1405
weighted avg 0.81 0.74 0.62 1405기준 모델, 로지스틱회귀 모델의 score은 0.74로 같지만, 기준 모델의 recall은 0으로 성능이 안 좋은 것을 확인 할 수 있다. 그에 비해, 로지스틱 회귀 모델의 recall은 0.78이다.
accuracy가 높다고 해서 좋은 성능 x , recall 고려!
# 참고
# 위에서 구한 test data의 classification_report와 비교하며 보기
precision_score(y_test, y_pred) >> 0.51
precision_score(y_test, y_pred, averege='binary') # default
>> 0.51 default값은 양성인 class의 값 반환해줌!
precision_score(y_test, y_pred, average=None) >> [0.90, 0.51] # [0확률, 1확률]
precision_score(y_test, y_pred, average='macro') >> 0.7
# macro_precision = (precision_class_1 + precision_class_2 + ... + precision_class_k) / class 개수(k)
precision_score(y_test, y_pred, average='weighted') >> 0.80 (두 샘플 수로 가중치를 두어 평균)
# weighted_precision = (precision_class_1 * n_class_1 + precision_class_2 * n_class_2 + ... + precision_class_k * n_class_k) / n_totalfrom sklearn.metrics import roc_curve, roc_auc_score
# Roc Curve
fpr, tpr, thresholds = roc_curve(y_val, y_pred_proba)
roc = pd.DataFrame({'FPR(Fall-out)':fpr,
'TPR(Recall)':tpr,
'threshold':thresholds})
roc.head()
>> FPR(Fall-out) TPR(Recall) Threshold
0 0.000000 0.000000 1.993953
1 0.000000 0.000196 0.993953
2 0.000000 0.000979 0.991687
3 0.000039 0.000979 0.991279
4 0.000039 0.001174 0.991045
# AUC score
auc = roc_auc_score(y_test, y_pred_proba)
auc
>> 0.81y_pred_proba는 분류 모델이 각 샘플이 양성(positive)에 속할 확률을 예측한 값.
0에 가까울수록 음성(negative)에 속할 확률이 높고 1에 가까울수록 양성에 속할 확률이 높다.
roc_auc_score에는 왜 predict가 아닌 predict_proba 함수를 사용해야할까?
- precision, recall과 같은 평가지표는 모델이 이미 분류하고 난 예측 범주(0 or 1)를 통해 점수를 계산한다.
- 하지만, AUC는 예측 범주가 아닌 예측 확률(1의 범주에 속할 확률)을 통해서 점수를 계산하는 평가지표이기 때문에 predict가 아닌 predict_proba 함수를 사용해야한다.
- 추가적으로, AUC는 이미 계산된 예측 확률로 점수를 계산하기 때문에 threshold에 따라 값이 바뀌지 않는다.
Roc curve를 이용하면 최적의 임계값 찾을 수 있다.
⇒ (0.5 threshold보다 더 좋은 성능을 낼 수 있겠지!)
# tpr, fpr차이가 최대가 되는 임계값 찾기
optimal_idx = np.argmax(tpr-fpr)
optimal_thresholds = thresholds[optimal_idx)
y_pred_default = y_pred_proba >= 0.5
y_pred_optimal = y_pred_proba >= optimal_threshold
classifiaciton report를 통해 recall값 확인
-> 최적화된 임계값이 더 좋은 recall 성능!!!!More Study
LogisticRegressionCV
모델 성능을 더 향상시키기 위해, 최적화해보자.
Cs: 로지스틱 회귀 모델의 규제 강도 조절하는 파라미터 (L1, L2 규제 강도 조절)
- Cs는 규제 매개변수 후보값인 C가 작아질수록, 규제가 강해지고, C가 커질수록 규제가 약해진다.
- Cs 리스트에 있는 모든 후보값에 대해 교차검증을 통해 최적의 C 찾아줌!
penalty 파라미터를 통해 규제 방법 지정 가능 (default = L2 규제)
from sklearn.linear_model import LogisticRegressionCV
model = LogisticRegressionCV(Cs=[0.001, 0.01, 0.1, 1, 10,100],
cv=5,
max_iter=1000)
model.fit(x_train, y_train)
model.C_ # 최적의 Cs값
>> [10.]
y_test_pred = model.predict(x_test)
- model.score(x_test, y_test)
- Regression : R2
- Classification : Accuracy
- predict없이 score 바로 사용 가능
df.drop_duplicates(keep=’first’)- keep=’first’ : 첫번째 중복값 유지, 나머지 중복값 삭제
- keep=’last’ : 마지막 중복값 유지, 나머지 중복값 삭제
- IQR (InterQuartile Range)
- 데이터 분포의 흩어진 정도를 측정하는 중요한 통계량 중 하나
- IQR이 클수록 데이터가 분산되어있다.
- IQR이 작을수록 데이터가 집중되어있다.
- oulier 탐지를 위해 IQR을 이용해, 범위 밖에 있는 데이터 찾기 가능
- 일반적으로, IQR*1.5를 벗어나는 값은 이상치로 간주
- box plot에서 활용됨. (min, Q1, median, Q3, max, oulier 시각적 표현)
- 데이터 분포의 중간 50% 범위를 측정하는 통계량 : Q1(제1분위수)와 제3분위수(Q3) 사이의 범위
- Q1 : data의 하위 25% 포함
- Q3 : data의 상위 25% 포함
- (median을 중심으로 상하 25%씩의 범위)
# 수치형 특성의 아웃라이어를 삭제해주겠습니다.
def outlier_iqr(data) :
q1, q3 = data.quantile([0.25, 0.75]) # Q1, Q3
iqr = q3 - q1
return q3 + (iqr*1.5)
# iqr*1.5를 벗어나는 값은 outlier로 간주
bmi_upper = outlier_iqr(df['BMI'])
ph_upper = outlier_iqr(df['PhysicalHealth'])
mh_upper = outlier_iqr(df['MentalHealth'])
sl_upper = outlier_iqr(df['SleepTime'])
# 네 개의 변수에서 oulier탐지하고, 해당 변수 중 하나라도 이상치를 가지는 행을 df에서 삭제
df = df[(df['BMI']<bmi_upper) | (df['PhysicalHealth']<ph_upper) | (df['MentalHealth']<mh_upper) | (df['SleepTime'] <sl_upper)]oulier가 포함된 데이터를 그대로 사용하면, 분석 결과가 왜곡되거나 부정확할 수 있으므로, 정확한 분석 결과를 얻기 위해 이러한 처리는 꼭 필요!
- pd.crosstab : 두 변수 간의 교차 테이블 생성
# 범주형 변수인 cat_featrues들과 타겟 변수인 'HeartDisease'변수 간의 관계 시각화
cat_features = ['Smoking','Stroke','DiffWalking','Sex','Diabetic','GenHealth']
fig = plt.figure(figsize=(30, 12))
for i, feature in enumerate(cat_features) :
tmp = pd.crosstab(index=df[feature], columns=df['HeartDisease'], normalize='index')
# nomalize : 각 범주형 변수 값이 차지하는 비율 계산해 테이블 정규화
# 범주형 변수 값이 서로 다른 비율을 가지는 경우에도, 정확한 비교 가능
ax = plt.subplot(2,3,i+1) # 2x3에 i+1번째 그래프 위치
tmp.plot(kind='bar', stacked=True, ax=plt.gca(), color = ['#4e7fc4', '#e68656'])
# plt.gca() : 현재 그래프의 축 객체 반환
# stacked=True : 각 범주형 변수의 값의 'HearDisease' 변수값 분포를 쌓아줌.
plt.xticks(rotation=0)
plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
i += 1
[Reference]
Logistic Regression
- StatQuest: Logistic Regression
- 로지스틱회귀와 선형회귀분석의 차이점이 무엇인가요?
- 5 Reasons “Logistic Regression” should be the first thing you learn when becoming a Data Scientist
- Logistic Regression Details Pt1: Coefficients
- Logistic Regression Details Pt 2: Maximum Likelihood
- Probability of passing an exam versus hours of study
Metrics for Classificaiton
- Making sense of the confusion matrix
- Machine Learning tips and tricks cheatsheet
- [Understanding AUC - ROC Curve](https://towardsdatascience.com/understanding-auc-roc-curve-68b2303cc9c5#:~:text=for multiclass model%3F-,What is AUC - ROC Curve%3F,capable of distinguishing between classes.)
- 3.3.2.14. Receiver operating characteristic (ROC)
- auc 참고자료
- sklearn.metrics.roc_curve
- sklearn.metrics.roc_auc_score
'Machine Learning' 카테고리의 다른 글
| [The Based Models 2] Boosting (0) | 2023.04.14 |
|---|---|
| [The Based Models 1] Tree Based Model (0) | 2023.04.14 |
| [Linear Models 3] Regularized Regression (0) | 2023.04.14 |
| [Linear Models 2] Generalization (0) | 2023.04.14 |
| [Linear Models 1] Linear Regression (0) | 2023.04.14 |



